Математичка задача стара еден век конечно решена: Како да се исече триаголник во квадрат?
По цели 122 години, една од најпознатите геометриски загатки – дали е можно да се исече рамностран триаголник и да се состави квадрат со истата површина користејќи најмал број делови – конечно доби одговор. И не само тоа: математичарите докажаа дека решение со помалку делови не постои.
Овој историски пробив го постигна тим од тројца истражувачи: Тонан Камата од Јапонскиот напреден институт за наука и технологија (JAIST), Рјухеи Уехара и Ерик Демејн од МИТ. Тие комбинираа алатки од теорија на графови и комбинаторна геометрија, применувајќи пристап инспириран од оригами и сложени алгоритми.

Содржина:
Од оригами до математика: иновативен пристап
Користејќи графови за да ги претстават рабовите и темињата на триаголникот и квадратот, научниците бараа совпаѓања меѓу патеките што ги формираат. Идејата била дека, доколку може да се пронајде идентична патека во двете фигури, тогаш би постоело решение со соодветен број на исечоци.
Првото ограничување било површината – и триаголникот и квадратот мора да имаат иста површина, бидејќи се составени од истите делови. Следно, се анализирала максималната должина на можното сечење. Дијагоналата на квадратот, која е неговиот најдолг можен пресек, сепак е пократка од страната на соодветен рамностран триаголник, што веднаш го исклучуваше дводелното решение.
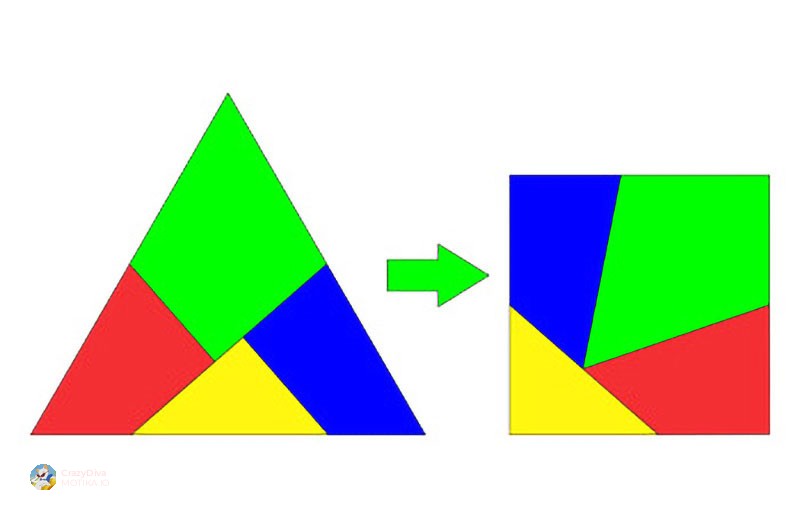
А троделно решение? Потешко отколку што изгледа.
Докажувањето дека троделно решение е невозможно било далеку посложено. „Постојат бесконечен број начини да се исече триаголник на три дела“, објаснува Демејн. „Секое парче може да има произволен број рабови, и координатите на сечењата можат да започнат од било каде. Затоа, компјутер не може едноставно да ги испроба сите можности.“
Тимот успеал да класифицира бесконечниот број можни сечења на триаголникот во пет категории, а за квадратот – 38 уникатни класификации. Потоа, ги споредиле графовите и патеките, барајќи совпаѓања според должина и агли.
Во сите обиди – нема совпаѓање. Со докази по контрадикција и развој на нови леми, тие заклучиле: не постои начин да се исече рамностран триаголник на три дела што ќе формира квадрат.
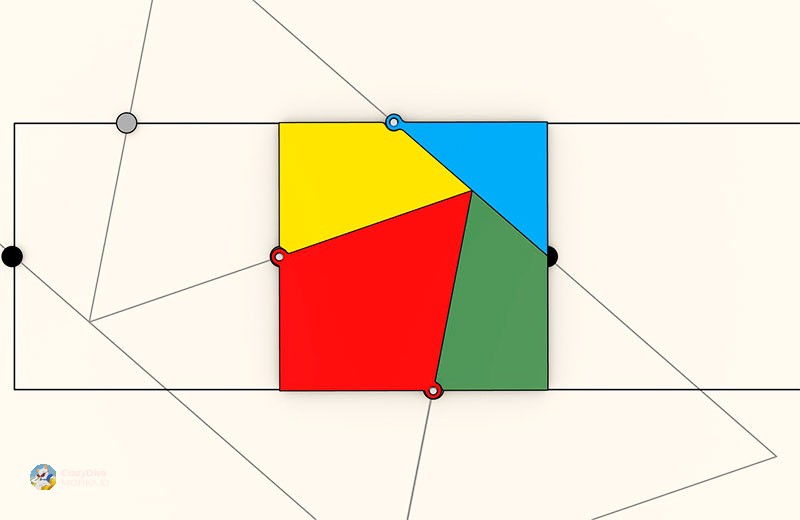
Повеќе од решение – нова алатка за математика
Иако загатката е решена, вредноста на нивниот труд оди подалеку. Методот на спојување на графови би можел да се примени и во други нерешени математички проблеми поврзани со дисекции, оригами и дури и оптимизација.
„Ако успееме да го поедноставиме доказот, можеби ќе отвориме пат за решавање и на други класични геометриски предизвици“, вели Демејн.
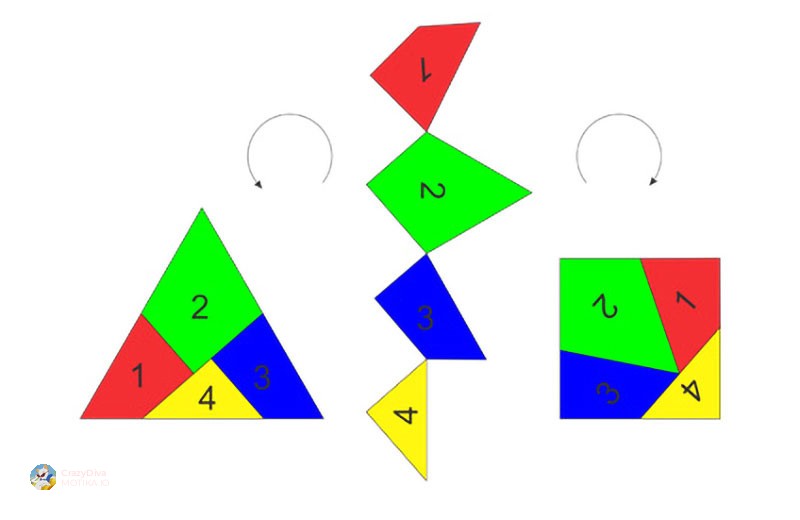







Коментирај анонимно